A Mathematical Model of Donor Kidney Cooling in Hypothermic Non-Perfusion Preservation

Introduction

Today, the growth in the number of patients waiting for various organ transplants makes it necessary to solve many problems associated with retrieval, temporary preservation and subsequent implantation of donor organs.

To preserve a donor kidney temporarily and, thereby, prolong its viability outside the organism within 36–72 h, two types of preservation have been developed: perfusion and nonperfusion [1, 2].

Non-perfusion preservation involves initial washing of the kidney from the blood and simultaneous cooling to a temperature of 20–25°C, which leads to inhibition of phosphorylation processes in the organ by 75%. Washing removes blood and prevents formation of blood clots, while simultaneous cooling promotes significant inhibition of metabolism in the organ, which is necessary for subsequent long-term extra-corporeal storage [3–6].

Washing is carried out using special preservative compounds, their ion composition being close to the intracellular fluid [4, 5]. Euro-Collins and Custodiol are the most popular solutions. After washing and cooling, the organs are put in a sterile package and then stored in a cold place at about 4°C [6].

Perfusion preservation involves the use of special perfusion machines to carry out arterial perfusion of the organ with a cooled oxygenated solution and simultaneous removal of oxidation products during transportation. As a result, it is possible to maintain high ATP level in cells, which in turn leads to preservation of cellular energy and membrane stabilization. Agents used as perfusates are cryoprecipitated plasma or salt solutions close to blood plasma in ion composition and contain albumin, plasma purified on silica gel and metabolites prolonging cellular metabolism under conditions of hypothermia [7–9].

Organ preservation using perfusion method is more physiological than non-perfusion one. However, perfusion preservation has certain limitations. Injury of the preserved organ caused at various perfusion stages is the main of them. Organ ischemia can result in perfusion nephropathy, which limits the time of effective preservation. Besides, this method is much more expensive and technically more complex than non-perfusion hypothermia.

It is easy to see that donor kidney cooling, which allows inhibition of metabolism in the organ, thereby prolonging its extra-corporeal storage, is common for both preservation methods. Improper cooling of donor kidneys inevitably leads to ischemic and then reperfusion injury of varying severity [1, 8, 10].

Unfortunately, so far, detailed investigation has been carried out only in relation to heat transfer process in cooling of thin renal tissue samples [11–13]. Thermophysics of cooling a kidney as a whole organ has been understudied due to renal tissue organization complexity making it difficult to carry out accurate experimental studies.

The aim of the study was to develop a mathematical model of donor kidney cooling and to compare the results obtained by using it to the experimental findings.

Materials and Methods

A mathematical model of kidney cooling. It is important to note that modeling of kidney cooling is no trivial task. This difficulty is determined by the complex structure of the organ, presence of complex internal components and the complex system of coolant flow.

In accordance with standard cooling technique, the liquid enters the kidneys through the renal artery, passes through the small arteries and capillaries and enters the filtering nephrons. The liquid is collected from the nephrons by the venous capillaries, then enters the small veins and is finally excreted from the kidney via the renal vein.

Due to complex structure of the kidney and the presence of a large number of channels with different diameters, creating a model requires finding answers to certain questions to ensure modeling accuracy. For example, what are the diameters of the channels through which the coolant flows, how important it is to take into account the exact geometry of these channels when creating a model.

Therefore, at the first stage of the investigation, there was an attempt to take into account the main features of cooling process in rough approximation.

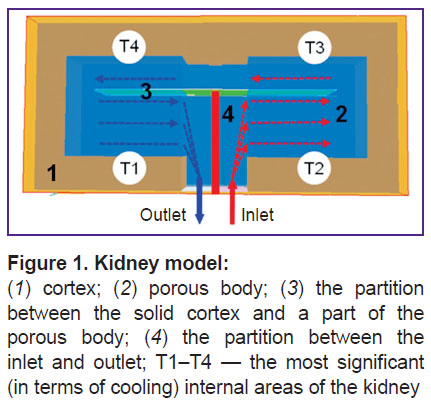
The developed mathematical model of cooling was based on a rather simple model of the kidney, consisting of the following parts: a thin solid cortex, a porous body, and two impermeable partitions washed over by the coolant (Figure 1).

---

Figure 1. Kidney model: (1) cortex; (2) porous body; (3) the partition between the solid cortex and a part of the porous body; (4) the partition between the inlet and outlet; T1–T4 — the most significant (in terms of cooling) internal areas of the kidney

---

This model suggests that the cooling process occurs as follows. The coolant first enters through the inlet artery into the right lower part of the porous body (area T2). The liquid flowing from this area around the inner partition enters areas T3 and T4. Flowing around the interior partition again, the liquid flows from area T4 to area T1, and then goes out of the kidney through the outlet vein. Thus, as a result of sequential passage of the coolant through areas T2–T4 and T1, the cooling liquid is heated, while the inner parts of the kidney are cooled.

The flow of coolant inside the proposed kidney model can be described by the system of Navier–Stokes equations for homogeneous porous media. In such media, the flow becomes steady much faster than its cooling occurs. Therefore, it is reasonable to assume that the task is steady and the following equation can be used to solve it:

where ρ is density; 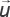is velocity vector; µ — dynamic viscosity coefficient; P —pressure; ξ — porous media resistance coefficient.

To determine the hydrodynamic parameters of the model (pressure distribution and velocity distribution inside the kidney), the equation (1) was solved numerically on a 50x42x122 Cartesian grid using the PHOENICS package [14]. The grid dimensions corresponded to the average dimensions of an adult kidney. The solid cortex thickness was 0.01 m.

Given that all working fluids applied to cool the kidney were similar to water in their thermal properties, ρ and µ values were taken for calculation from the corresponding tabular data for water.

Special experiments were carried out to determine porous media resistance coefficient. Coolant pressure at the arterial entrance into the kidney was recorded, its consumption measured. The following coefficient value was obtained during the experiments: ξ=0.00248.

Pressure and velocity distributions were also calculated (Figure 2).

---

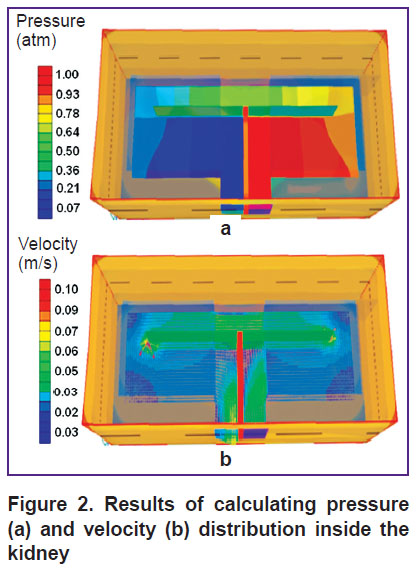
Figure 2. Results of calculating pressure (a) and velocity (b) distribution inside the kidney

---

As it can be seen from the figures, coolant pressure and velocity distributions inside the kidney correspond to the flow in a porous medium: pressure and velocity have the highest values at the inlet and fall slowly as the fluid moves through the porous body to the outlet. In this case, distribution of coolant velocity is determined by the geometry of the area through which it flows (see Figure 1).

Energy equation was used to solve the task of kidney cooling:

where С_P is heat capacity at constant pressure; λ — thermal conductivity coefficient; T — temperature.

The boundary conditions for equation (2) are the boundary conditions of the third kind on all boundary surfaces:

where 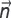— normal to the surface; α — heat transfer coefficient; T_am — the ambient temperature taken as 22°C.

The heat transfer coefficient α is selected for each kidney surface, taking into account that heat transfer in the ambient air is induced by natural convection.

The cooling task was solved taking into account indices corresponding to standard cooling technique parameters: coolant flow rate — 15 ml/min; fluid temperature — 4–13°С; arterial pressure — 90–110 mm Hg.

Calculation of time-dependent cooling and temperature changes in different parts of the kidney was performed using the PHOENICS package on the same grid as that for calculation of hydrodynamic flow parameters. Velocity distribution in the calculation of cooling was considered steady and corresponding to the velocity distribution calculated at the stage of determining the hydrodynamic parameters of the model. Calculation convergence and heat balance were controlled with respect to time at each step. Heat balance was calculated with accuracy of at least 10^–5, which was rather a good value.

The following thermal parameter values were used in calculations: thermal conductivity coefficient λ=0.55 W/(m·K), heat transfer coefficient α=10 W/(m²·K). Given that all working fluids applied to cool the kidney are similar to water in their thermophysical properties, other physical parameters were taken from the corresponding tabular data for water.

The results of calculating time-dependent temperature distribution in the horizontal plane passing through the middle of the kidney are shown in Figure 3.

---

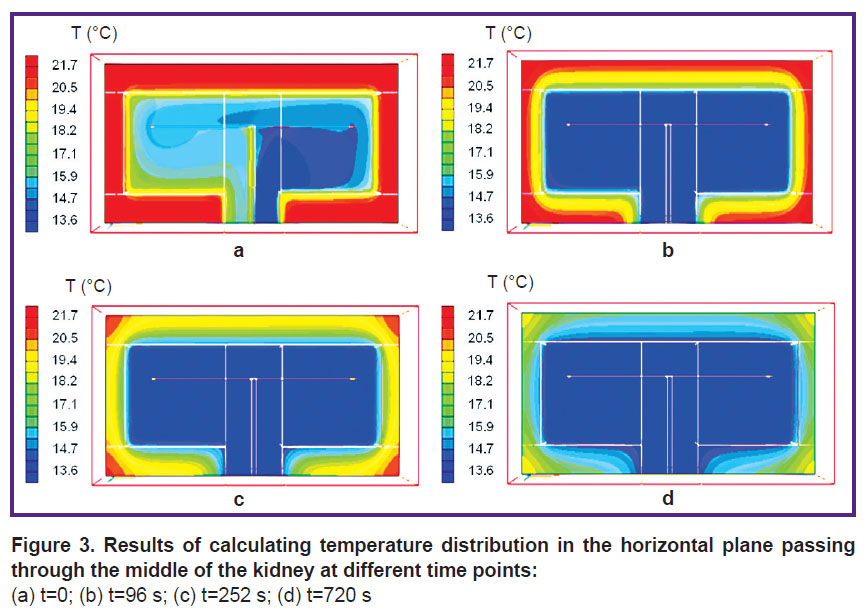
Figure 3. Results of calculating temperature distribution in the horizontal plane passing through the middle of the kidney at different time points: (a) t=0; (b) t=96 s; (c) t=252 s; (d) t=720 s

---

The figure clearly shows that in the proposed model, temperature of different kidney areas changes at different rates. The inner porous body cooled most rapidly, area T2 cooling quicker than other parts of the porous body (see Figure 1), while area T1 was the slowest to cool. The solid cortex was the area cooled the longest of all. In the proposed model, uneven cooling of different areas of the kidney can be explained by the fact that rapid cooling occurs in those places where the fluid flows. The remaining parts of the kidney are cooled by heat transfer process, which always provides slower cooling than convective heat exchange.

Comparison of calculated data with experimental findings. The adequacy of the mathematical model of kidney cooling was assessed by comparing the calculation results with the experimental findings. For this purpose, there was created a mobile experimental installation whose components are shown in Figure 4.

---

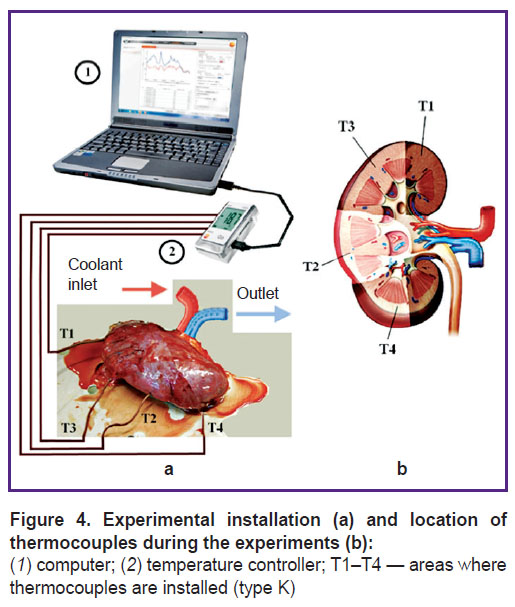
Figure 4. Experimental installation (a) and location of thermocouples during the experiments (b): (1) computer; (2) temperature controller; T1–T4 — areas where thermocouples are installed (type K)

---

The most important component of the installation is a four-channel temperature meter (controller) Testo 176 (Testo, Germany) with the following characteristics: measurement range — from –195 to +1000°C; error — ±0.3°C; resolution — 0.1°C.

The experiments were carried out on cadaver kidneys obtained from donors who died a violent death. When retrieving the kidneys, the body temperature was 20–25°C.

Prior to the beginning of each experiment, four thermocouples were installed in different places inside the kidney at 8–10 mm depth. Locations of the thermocouples corresponded to the areas shown in Figure 1. Next, a container with a cooling solution of Custodiol was installed 120–140 cm above the kidney level and connected to the renal artery, cooling was initiated according to the standard procedure. The initial temperature of the solution was 13°C.

During the experiments, the temperature controller took readings of thermocouples successively with 1 min interval and recorded them in its internal memory first and then in the computer memory. The data were processed using special software and displayed on the screen.

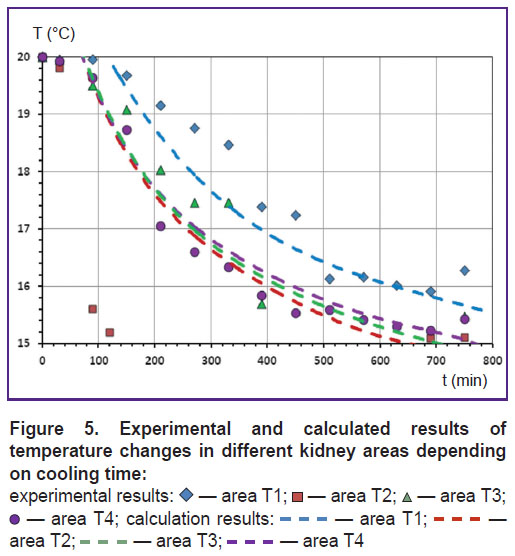
For example, Figure 5 presents experimental and calculated results of temperature changes in different parts of the kidney depending on the cooling time. Experimental results show that cooling the kidney by standard methods ensures no cooling uniformity. The cooling rate of different areas was different. Area T2 cooled the most rapidly compared to others, area T1 was the slowest to cool.

---

Figure 5. Experimental and calculated results of temperature changes in different kidney areas depending on cooling time: experimental results: — area T1; — area Т2; — area Т3; — area Т4; calculation results: — area Т1; — area Т2; — area Т3; — area Т4

---

Cooling of areas T3 and T4 occurred at approximately the same rate, it was less than the cooling rate of area T2, but more than that of area T1. The same tendency was observed in the calculated results presented in the figure: different areas of the kidney cooled at different rates.

Using the proposed method, calculations were carried out for two values of thermal conductivity coefficient: λ=0.55 W/(m·K) and λ=0.4 W/(m·K). Comparison of calculation results for areas T1, T3, and T4 with the experimental ones allowed making a conclusion that calculations at λ=0.55 W/(m·K) were closer to experimental results. Besides, the obtained value of λ=0.55 W/(m·K) is in good agreement with the results of Kulikov and Syakterev [13] who experimentally obtained value λ=0.3–0.6 W/(m·K) for thin layers of renal tissue in a wide temperature range. Significant difference between the calculated and experimental results for area T2 can be attributed to insufficient regard for kidney structure details in the proposed computational model.

Conclusion

Proper cooling of the donor kidney provides the possibility to inhibit the metabolism of the organ significantly and thereby extend the storage time for subsequent transplantation. The longer the preservation time, the more patients in need of transplantation can be provided with necessary medical care. Therefore, mathematical modeling and experimental study of thermal physics of cooling the kidney as a whole organ play an important role.

It is necessary to underline that modeling of kidney cooling is no easy task, the difficulty of which is determined by complex structure of the organ and coolant flow particulars. With this in mind, the authors have developed a model that takes into account only the main features of the cooling process at this stage. However, even in this simple formulation of the problem, it is possible to establish using the model that the standard method of cooling the kidney ensures no cooling uniformity: the cooling rate of different areas appears to be different.

The developed mathematical model makes it possible to find the temperature and time of cooling for different kidney areas using cooling solutions with different initial temperatures and different thermal properties. It allows us to evaluate cooling solutions without additional experiments.

The values of porosity coefficient ξ=0.00248 and thermal conductivity coefficient λ=0.55 W/(m·K) obtained using the model can be applied in development of new cooling methods.

Acknowledgements. The authors would like to thank the management of N.V. Sklifosovsky Research Institute of Emergency Care for their interest in the work and assistance in performing the experiments.

Study funding. The study was supported by the grant of the Russian Science Foundation (project No.18-19-00615)

Conflict of interests. The authors have no conflict of interests to disclose.