Статистическая классификация иммуносигнатур для задач ранней диагностики заболеваний при значительном сокращении размерности признакового пространства
Цель исследования — оценить возможности существенного сокращения признакового пространства иммуносигнатурных данных с помощью отбора наиболее информативных признаков при сохранении достаточного качества классификации заболеваний человека по этим данным.
Материалы и методы. Технология иммуносигнатуры основана на применении пептидных микрочипов, в которых пептиды со случайными аминокислотными последовательностями используются для обнаружения болезней. Такие пептиды служат частичным или полным подобием эпитопов антигенов. Определение заболеваний производится при помощи алгоритмов классификации, обученных на редуцированной выборке иммуносигнатурных паттернов пациентов с известными диагнозами.
Данные. Для проведения экспериментов использовались иммуносигнатурные данные, полученные на основе применения пептидного микрочипа высокого разрешения, имеющего порядка десяти тысяч пептидных ячеек. Оцифрованные данные для формирования выборок получены из публичной базы данных NCBI (идентификатор GSE52580).
Методы поиска информативных признаков. Для сокращения размерности признакового пространства производился поиск информативных пептидов. С этой целью проверялись применимость различных статистических критериев и меры разделимости классов, таких как t-критерий Стьюдента, U-критерий Манна–Уитни–Вилкоксона, Колмогорова–Смирнова, расстояние Джеффриса–Матуситы.
Методы классификации. Использовались классификаторы, основанные на различном математическом аппарате: метод опорных векторов, наивный байесовский классификатор, случайный лес, градиентный бустинг.
Оценка качества классификации. Использовалась метрика доли правильных ответов, которая применяется как для бинарной, так и для мультиклассовой классификации.
Результаты. Экспериментальные исследования показали, что сокращение размерности и поиск информативных пептидов — необходимая мера, которая позволяет существенно сократить время работы классификаторов — от 16 до 1625 раз, а также сократить признаковое пространство в 240 раз без потери качества классификации. Показано, что все рассмотренные классификаторы с равным успехом справляются с задачей классификации иммуносигнатур.
Заключение. Результаты работы демонстрируют перспективность применения разработанного подхода к сокращению исходного размера признакового пространства иммуносигнатурных данных для более быстрой классификации без потери ее точности.
Введение
Сегодня распространенность онкологических, инфекционных и других заболеваний сохраняется на достаточно высоком уровне [1]. При этом диагностика таких заболеваний до сих пор остается достаточно дорогостоящей и длительной процедурой, отличающейся множеством недостатков. Традиционная диагностика онкологических заболеваний распознает болезни в основном на поздней стадии, когда вероятность излечения крайне низка [2]. Поэтому сейчас в мировом сообществе проводится активная работа по поиску новых методов ранней диагностики опасных заболеваний, одним из которых является технология иммуносигнатуры [3].
Данная технология основана на применении пептидных микрочипов, где пептиды со случайными аминокислотными последовательностями используются для обнаружения болезней [4]. Данные пептиды служат частичным или полным подобием эпитопов антигена. Использование множества пептидов, представляющих собой вероятные аминокислотные последовательности белков, делает возможным определение связывающего партнера для многих антител, даже если точное совпадение для эпитопа отсутствует [5]. Именно эти данные могут помочь в постановке окончательного диагноза.
На сегодняшний день существует несколько видов пептидных матриц, содержащих от 10 тыс. до 350 тыс. пептидов [6, 7]. Из-за большого количества признаков возникает проблема анализа и интерпретации таких данных. Даже опытному специалисту очень непросто поставить диагноз, анализируя значения матрицы с тысячами различных пептидов [8, 9]. Возможное решение проблемы — автоматическая классификация данных. Однако классификация данных больших размерности и объема весьма трудоемка и требует немалых вычислительных ресурсов. Одним из решений данной проблемы является использование не всех доступных пептидов, а только наиболее информативных. Благодаря такому подходу возможно уменьшение признакового пространства в десятки раз при сохранении достаточно высокого качества классификации. Существует множество методов отбора наиболее информативных признаков-пептидов, однако, согласно исследованиям [10], наиболее практически значимым являетя t-критерий Стьюдента.
Цель исследования — оценка эффективности использования классификации иммуносигнатурных данных при значительном уменьшении признакового пространства с выделением наиболее информативных признаков при сохранении достаточного качества классификации.
В связи с этим в данной работе решаются следующие задачи:
значительное сокращение признакового пространства с помощью различных методов и выделение при этом наиболее информативных признаков;
оценка различных классификаторов для иммуносигнатурных данных с целью нахождения наиболее эффективного метода сокращения размерности.
Материалы и методы
Данные. В исследовании использовалась технология, основанная на применении пептидного микрочипа [11]. Оцифрованные данные были получены из публичного хранилища биомедицинских данных GEO [12]:
количество экземпляров (пациентов) — 240;
количество пептидов — 9781;
количество классов — 6.
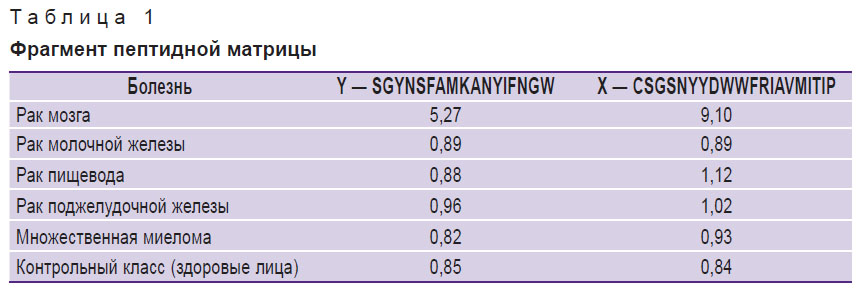
В табл. 1 представлен фрагмент оцифрованной пептидной матрицы с известными классами болезней Y и пептидами X. Названия пептидов представлены в виде последовательности составляющих их аминокислот.
|
Таблица 1. Фрагмент пептидной матрицы |
Методы поиска информативных признаков. Для решения задачи отбора наиболее информативных признаков целесообразно рассмотреть использование различных статистических тестов и меры разделимости классов. В данной работе используются различные (параметрические и непараметрические) критерии:
t-критерий Стьюдента [13];
U-критерий Манна–Уитни–Вилкоксона [14];
критерий Колмогорова–Смирнова [15];
расстояние Джеффриса–Матуситы [16].
При использовании любого статистического теста выдвигается две противоположные гипотезы. Одна называется альтернативной гипотезой (ее обозначают H1), другая — нулевой (обозначается H0). В нашем исследовании мы предположили следующее: нулевая гипотеза говорит о том, что классы, представленные в табл. 1, неразделимы, а альтернативная — о том, что классы разделимы.
Статистические тесты, используемые в данной работе, направлены на парное сравнение двух различных классов. Поэтому выбран контрольный класс (здоровые лица), который попарно сравнивался с классами болезней (см. табл. 1). В результате получается пять независимых выборок (контрольный класс против каждого типа рака) для каждого теста. Для оценки работы каждого статистического критерия используется р-значение.
P-значение (p-value) — это мера, приеняемая при тестировании статистических гипотез. Фактически это вероятность ошибки при отклонении нулевой гипотезы. Обычно при исследованиях р-значение сравнивают с общепринятыми стандартными уровнями значимости р=0,05 или р=0,01 [17]. В нашем исследовании будем считать пептид информативным при р<0,005. Из-за большого количества признаков-пептидов для формирования выборок отбирались пептиды с минимальным р-значением.
Методология отбора информативных пептидов для статистических тестов:
для каждого теста формируем пять независимых выборок сравнений каждого типа рака с контрольным классом;
из каждой выборки отбираем N пептидов, имеющих минимальное p-значение;
объединяем полученные выборки в один набор без повторений пептидов.
Для применения критерия расстояния Джеффриса–Матуситы необходимо отобрать только те пептиды, которые имеют максимальное расстояние.
Методология отбора информативных пептидов для расстояния Джеффриса–Матуситы:
формируем пять независимых выборок сравнений каждого типа рака с контрольным классом;
объединяем полученные выборки в один набор без повторений пептидов;
отбираем N пептидов, имеющих максимальное значение расстояния Джеффриса–Матуситы.
Методы классификации. Существует огромное количество различных методов классификации данных, которые могут быть опробованы для решения этой задачи. Поэтому целесообразно выбрать классификаторы, основанные на разном математическом аппарате. Рассмотрим кратко наши классификаторы:
Метод опорных векторов (support vector machine, SVM) — один из часто используемых алгоритмов обучения с учителем, применяется для решения задач классификации и регрессионного анализа. Принадлежит к семейству линейных классификаторов. Из-за своей универсальности имеет широкое применение в медицине, финансах, для распознавания образов и в других областях [18].
Наивный Байес (naive Bayes classifier, NB) — вероятностный классификатор, основанный на теореме Байеса со строгими (наивными) предположениями о независимости между признаками [19]. Основное его достоинство — простота реализации и низкие вычислительные затраты при обучении. Недостаток — низкое качество классификации в задачах c высокой размерностью признаков.
Случайный лес (random forest, RF) — алгоритм машинного обучения, использующий комитет (ансамбль) решающих деревьев [20]. Главная идея алгоритма заключается в том, что строится множество разных моделей с участием относительно слабого алгоритма, результат предсказаний каждой модели усредняется и выбирается лучшее решение. Главное преимущество RF — это способность эффективно обрабатывать данные с большим числом признаков и классов.
Градиентный бустинг (extreme gradient boosting, Xgboost) — алгоритм машинного обучения, заключающийся в построении линейной комбинации простых алгоритмов путем изменения веса входных данных [21–22]. Каждая последующая модель (как правило, дерево решений) строится таким образом, чтобы придавать больший вес и отдавать предпочтение ранее некорректно предсказанным наблюдениям.
Оценка качества классификации. В задачах машинного обучения для оценки качества моделей и сравнения различных алгоритмов используются метрики, а их выбор и анализ — непременная часть любого исследования. Для определения основных метрик используем матрицу ошибок (confusion matrix) [23], которая представлена в табл. 2.

|
Таблица 2. Матрицы ошибок |
Здесь ŷ — это ответ алгоритма на объекте, а y — истинная метка класса на этом объекте.
Для оценки качества классификации используются различные метрики:
accuracy (доля правильных ответов);
precision (точность);
recall (полнота);
F-score (F-мера).
В нашем исследовании мы используем наиболее распространенную метрику — долю правильных ответов, которая применяется как для бинарной классификации, так и для мультиклассовой.
Методика классификации. Классификация данных производится в несколько этапов:
применение схемы скользящего контроля [24], которая базируется на десятикратном разбиении множества объектов, разделение случайным образом исходной выборки данных на обучающую и тестовую в равных пропорциях;
обучение классификатора на обучающей выборке и проверка его на тестовой;
оценка качества классификации с использованием одной из описанных метрик.
Результаты
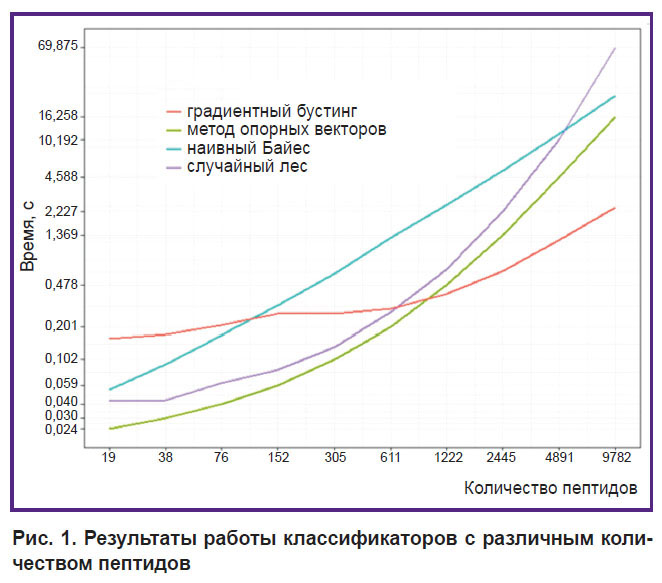
Для обработки пептидных матриц выдвигаются значительные требования как к процессорной мощности, так и к оперативной памяти. На рис. 1 представлен график сравнения времени (логарифмическая шкала) обучения классификаторов с различным количеством пептидов. Легко заметить, что при уменьшении количества пептидов скорость обучения многократно возрастает. Все это приводит к тому, что обучение модели становится доступно даже на стандартном компьютере. Поэтому сокращение признаков в иммуносигнатуре — это важный этап, который позволяет корректно оценивать результаты.
|
Рис. 1. Результаты работы классификаторов с различным количеством пептидов |
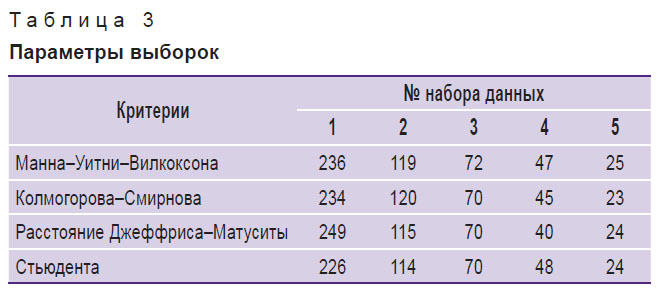
В табл. 3 представлены объемы выборок, полученных в результате отбора соответствующим методом. В результате получается пять выборок с разным количеством пептидов.
|
Таблица 3. Параметры выборок |
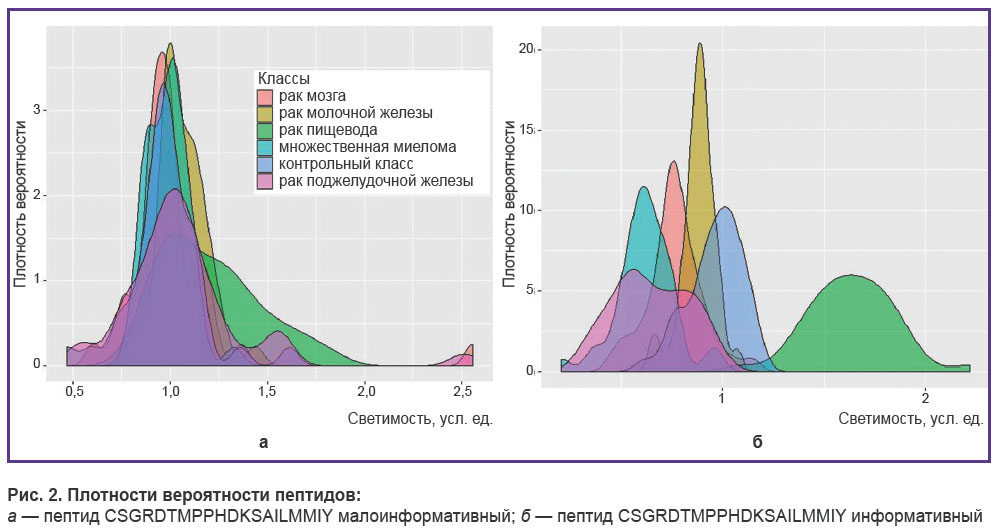
Для оценки корректности работы методов построим сглаженную диаграмму частот для наиболее и наименее информативного пептида. На рис. 2, а изображен пептид, который выбран методом Джеффриса–Матуситы как малоинформативный. Значения светимостей у всех классов болезней похожи, поэтому данный пептид бесполезен для классификации, так как вносит шум в признаковое пространство. На рис. 2, б изображен пептид, который выделяется как информативный, при этом заметны явные отличия между классами. Поэтому данный пептид пригоден для использования в алгоритмах классификации.
|
Рис. 2. Плотности вероятности пептидов: а — пептид CSGRDTMPPHDKSAILMMIY малоинформативный; б — пептид CSGRDTMPPHDKSAILMMIY информативный |
Полученные результаты позволяют заключить, что отбор информативных признаков — это важная процедура при анализе данных иммуносигнатур, которая позволяет существенно снизить размерность признакового пространства, «очистив» его от избыточных, неинформативных данных.
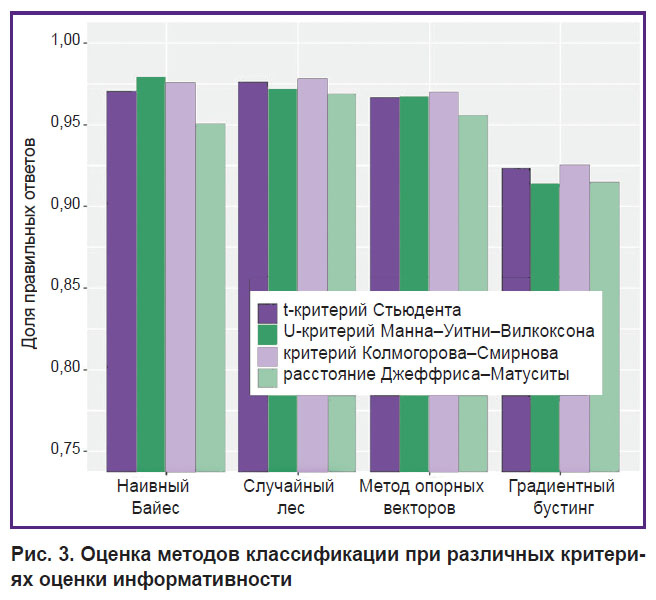
Результаты классификации представлены на рис. 3. Для оценки работы классификаторов использован набор данных №1 из табл. 3, для оценки качества классификации — метрика доли правильных ответов (accuracy). Отметим, что все критерии отбора информативных признаков показали достаточно хорошее качество классификации, которое не зависит от типа классификатора. Следует сказать, что для классификации иммуносигнатур возможно применение широкого набора доступных классификаторов.
|
Рис. 3. Оценка методов классификации при различных критериях оценки информативности |
Следующий этап эксперимента — это детальное рассмотрение каждого из методов сокращения размерности. Ввиду незначительных отличий между классификаторами для проведения дальнейшего исследования остановимся на одном из рассмотренных алгоритмов классификации, а именно на алгоритме «случайный лес».
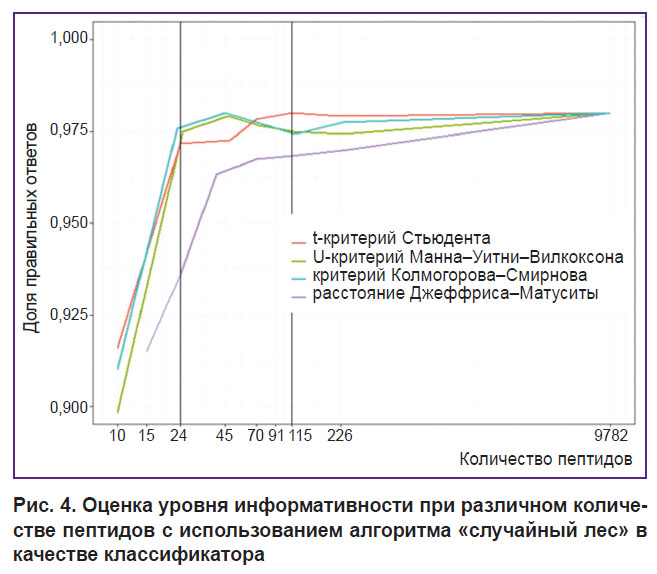
На рис. 4 представлен график тестирования с помощью алгоритма «случайный лес» различных выборок из табл. 3. Каждая точка на графике представляет собой среднее значение доли правильных ответов после десятикратного обучения алгоритма «случайный лес». Анализируя результаты тестирования, следует отметить, что при количестве пептидов меньше 24 качество классификации начинает снижаться, а при увеличении их количества до 115 качество классификации не растет. Полученная область информативности расположена между этими двумя границами.
|
Рис. 4. Оценка уровня информативности при различном количестве пептидов с использованием алгоритма «случайный лес» в качестве классификатора |
Рассмотренные методы отбора информативных признаков дают корректный результат, и на выборке с малым количеством признаков можно достигнуть качества классификации, сравнимого с классификацией на исходной выборке.
Заключение
В связи с бурным развитием современных технологий ранней диагностики заболеваний возникает проблема анализа данных большой размерности. Новые технологии позволяют получать большое количество признаков с различной диагностической ценностью, что обусловливает необходимость анализа и отбора наиболее информативных из них.
В рамках исследования экспериментально доказано, что с помощью рассмотренных методов сокращения размерности можно выделить наиболее информативные признаки-пептиды. В результате удается сократить признаковое пространство без потери качества классификации примерно в 240 раз. При этом время работы классификаторов удается уменьшить в 16 раз для градиентного бустинга и в 1625 раз — для случайного леса, благодаря чему задача классификации может быть решена и на компьютерах со стандартными характеристиками.
В результате эксперимента не выявлен явный лидер как в методах классификации, так и в методах поиска информативных признаков. Рассмотренные методы сокращения размерности и классификации в дальнейшем будут использоваться и с другими пептидными матрицами более высокой размерности.
Финансирование исследования. Исследование не финансировалось какими-либо источниками.
Конфликт интересов. У авторов нет конфликта интересов.
Литература
- World Cancer Report 2014. Geneva: World Health Organization, International Agency for Research on Cancer; 2014.
- Ntagirabiri R., Munezero B., Nizigiyimana G., Ngomirakiza J.B., Ndabaneze E. Assessment of diagnostic efficiency of the optic upper digestive endoscopy in the era of video endoscopy. Journal Africain d’Hépato-Gastroentérologie 2015; 9(2): 64–67, https://doi.org/10.1007/s12157-015-0587-7.
- O’Donnell B., Maurer A., Papandreou-Suppappola A., Stafford P. Time‑frequency analysis of peptide microarray data: application to brain cancer immunosignatures. Cancer Inform 2015; 14(2): 219–233, https://doi.org/10.4137/cin.s17285.
- Richer J., Johnston S.A., Stafford P. Epitope identification from fixed-complexity random‑sequence peptide microarrays. Mol Cell Proteomics 2015; 14(1): 136–147, https://doi.org/10.1074/mcp.m114.043513.
- Kukreja M., Johnston S.A., Stafford P. Immunosignaturing microarrays distinguish antibody profiles of related pancreatic diseases. J Proteomics Bioinform 2012; 1(S6): 001, https://doi.org/10.4172/jpb.s6-001.
- Stafford P., Cichacz Z., Woodbury N.W. Immunosignature system for diagnosis of cancer. Proc Natl Acad Sci USA 2014; 111(30): E3072–E3080, https://doi.org/10.1073/pnas.1409432111.
- Singh S., Stafford P., Schlauch K.A., Tillett R.R., Gollery M., Johnston S.A., Khaiboullina S.F., De Meirleir K.L., Rawat S., Mijatovic T., Subramanian K., Palotás A., Lombardi V.C. Humoral immunity profiling of subjects with myalgic encephalomyelitis using a random peptide microarray differentiates cases from controls with high specificity and sensitivity. Mol Neurobiol 2016; 55(1): 633–641, https://doi.org/10.1007/s12035-016-0334-0.
- Шаповал А.И., Легутки Д.Б., Стаффорд Ф., Требухов А.В., Джонстон С.А., Шойхет Я.Н., Лазарев А.Ф. Иммуносигнатура — пептидный микроэррей для диагностики рака и других заболеваний. Российский онкологический журнал 2014; 19(4): 6–11.
- Осипова Т.В., Рябых Т.П., Барышников А.Ю. Диагностические микрочипы: применение в онкологии. Российский биотерапевтический журнал 2006; 5(3): 72–81.
- Андрющенко В.С., Перец Е.Ю., Лялюхова И.Е. Классификация иммуносигнатурных данных для задач ранней диагностики опасных заболеваний. В кн.: Информационные технологии и математическое моделирование (ИТММ-2017). Томск; 2017; c. 18–25.
- Stafford P., Halperin R., Legutki J.B., Magee D.M., Galgiani J., Johnston S.A. Physical characterization of the “immunosignaturing effect”. Mol Cell Proteomics 2012; 11(4): M111.011593, https://doi.org/10.1074/mcp.m111.011593.
- GSE52580. URL: https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE52580.
- Student. The probable error of a mean. Biometrika 1908; 6(1): 1–25, https://doi.org/10.2307/2331554.
- Mann H.B., Whitney D.R. On a test of whether one of two random variables is stochastically larger than the other. The Annals of Mathematical Statistics 1947; 18(1): 50–60, https://doi.org/10.1214/aoms/1177730491.
- Salvia A.A. Some fundamental properties of Kolmogorov–Smirnov consonance sets. Technometrics 1980; 22(1): 109–111, https://doi.org/10.2307/1268389.
- Matusita K. Statistical theory and data analysis. Biometrics 1985; 41(3): 815, https://doi.org/10.2307/2531311.
- Cumming G. Replication and p intervals: p values predict the future only vaguely, but confidence intervals do much better. Perspect Psychol Sci 2008; 3(4): 286–300, https://doi.org/10.1111/j.1745-6924.2008.00079.x.
- Mammone A., Turchi M., Cristianini N. Support vector machines. Wiley Interdisciplinary Reviews: Computational Statistics 2009; 1(3): 283–289, https://doi.org/10.1002/wics.49.
- Shaik L., Swamy N.N. Efficient implementation of class based decomposition schemes for naive bayes classifier. International Journal of Science and Research 2015; 4(11): 237–240, https://doi.org/10.21275/v4i11.nov151091.
- Breiman L. Random forests. Machine Learning 2001; 45(1): 5–32, https://doi.org/10.1023/a:1010933404324
- Natekin A., Knoll A. Gradient boosting machines, a tutorial. Front Neurorobot 2013; 7: 21, https://doi.org/10.3389/fnbot.2013.00021.
- Friedman J.H. Greedy function approximation: a gradient boosting machine. Ann Statist 2001; 29(5): 1189–1232, https://doi.org/10.1214/aos/1013203451.
- Ting K.M. Covariance Matrix. In: Sammut C., Webb G. (editors). Encyclopedia of machine learning and data mining. Boston, МА: Springer; 2016, https://doi.org/10.1007/978-1-4899-7502-7_50-1.
- Sylvain A., Celisse A. A survey of cross-validation procedures for model selection. Statistics Surveys 2010; 4(0): 40–79, https://doi.org/10.1214/09-ss054.










